Graph2Go - Diagrama Skaičiuotuvai yra instrumentinė mokymo ir mokymosi matematika. Tai aplinka, kuri palaiko konceptualų supratimą apie funkcijas apskritai, ir mokyklos algebros ir nekilnojamojo analizę, visų pirma. Ypač, jis pagerina ryšius tarp grafikos ir simbolinę išraišką. Pagrindinis tikslas algebros mokymo yra aprūpinti besimokančiuosius su įrankiais mathematize savo suvokimą. Multi-reprezentacinės požiūris turi potencialą perkelti sprendžiant net tradicinių problemų iš priskiriant ir spręsti dėl nežinomos analizuoti įvairias procesus ir santykius tarp šių procesų dėmesio. Iš kelių atstovybių funkcijos integravimas sukuria galimybes plėtoti įvairesnių sprendimų metodų tradicinių problemų. Priartinimas ant grafikų skaičiuotuvas naudoti, mokslininkai nurodo keturis modelius ir būdus naudoti: skaičiuojamasis įrankių, duomenų analizės įrankis, vizualizavimo įrankis, ir tikrinimo įrankis.
Dinaminis transformacijos yra unikalus įrenginys iš Graph2Go.Dinaminis kontrolė apima tiesioginį manipuliavimą objekto ar matematinę objekto atstovavimo. Kaip vairuoti indėlis yra raidė-simbolinis vienas, transformacijas atliekami numerių dalyvauja funkcijos išraiška. Taigi, iš to parameterizing pavyzdį mes ją paversti funkcijų šeimos. Tyrimai rodo, kad Sensation ryšys tarp vartotojo ir objekto ekrane gali turėti svarbų vaidmenį plėtojant gilesnį supratimą apie matematinės sąvokos.
Pagrindinės savybės Graph2Go:
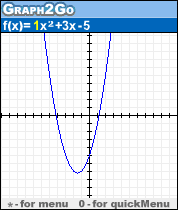
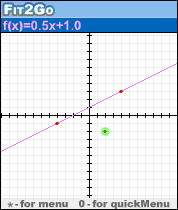
* Grafikai vienišų kintamųjų funkcijos išraiškos.
* Dinaminis grafikų transformuotų išraiškos.
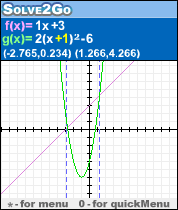
* Lankytinos vietos (didžiausias, mažiausias, inflection_ yra pažymėtos ir jų skaitinės vertės pateiktos.
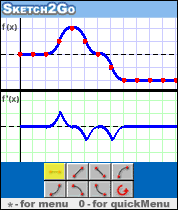
* Diagrama ir išraiška išvestinės funkcija.
* Diagrama, išraiška sudėtinė funkcija šeimai.
* Plotas iki tam tikros funkcijos integralas, išreiškiamas.
* Mastelio keitimas ir PERSKAIČIAVIMĄ variantų.Graph2Go yra specialios paskirties grafikų skaičiuotuvas, kuri veikia už suteiktas rinkinių funkcijos išraiškos. Nurodytos šeimos funkcijos išraiškos ir įrankiai, kurie palaiko paprastus pakeitimus bet pavyzdyje buvo skirta greitam ir lengvam naudojimui su nedideliu klaviatūra.
Siūlomi užsiėmimai "
Žemiau yra įdomus pavyzdys, kad sujungia vizualinio mąstymo naudojimą su analitinės užduotį ir turi potencialą didinti procesinius veiksmus su konceptualaus supratimo:
Įrodyti arba paneigti kiekvieną iš šių teiginių.
Paaiškinti ir įrodyti savo metodą ir atsakyti naudojant Graph2Go, popieriaus ir pieštuką, arba psichikos operacijas
* Iš funkcijų šeimos darinys gali būti ne vienas funkcija.
* [K * f (x)] "yra lygus k * [f (x)]"
* [K * (f (x)] "yra lygus [f (kX)]"
Jei studijuoti skaičiavimas su grafinius kalkuliatorių paramos žr AP (Išplėstinė Talpinimo) skaičiavimas svetainę pavyzdžių skaičiavimas įvertinimo problemos (atliekami su arba be grafikų įrankiai).
Kas naujo šioje versijoje:
& Middot; Piešimas taupymas
& Middot; Pašto dėžutę
& Middot; Nustatymai& Middot; Patobulintos grafika
& Middot; klaidų pataisymai
Taikymo informacija:
Versija: 0.84
Įkėlimo datą: 28 Apr 11
Kūrėjas: Math4Mobile
Licencija: Nemokamai
Populiarumas: 352
Dydis: 104 Kb


Komentarai nerastas